This class will create a smooth surface that approximates a two-argument function F(X,Y) from a given set of samples of that function on a rectangular grid with regular or irregular spacing. More...

Classes
class	PatchHint
	This object is used to hold precalculated data about the most recently accessed patch to accelerate the common case of repeated access to the same patch or to nearby patches. More...

Public Member Functions
	BicubicSurface ()
	Construct an uninitialized BicubicSurface handle. More...

	~BicubicSurface ()
	Destructor deletes the underlying surface if there are no more handles referencing it, otherwise does nothing. More...

	BicubicSurface (const BicubicSurface &source)
	Copy constructor makes a shallow copy of source; the new handle will reference the same underlying surface as does source. More...

BicubicSurface &	operator= (const BicubicSurface &source)
	Copy assignment is shallow; it makes this handle reference the same underlying surface as does source. More...

	BicubicSurface (const Vector &x, const Vector &y, const Matrix &f, Real smoothness=0)
	Construct a bicubic surface that approximates F(X,Y) given samples f(i,j) with the sample locations in f defined by the vectors x and y. More...

	BicubicSurface (const Vec2 &XY, const Vec2 &spacing, const Matrix &f, Real smoothness=0)
	Construct a bicubic surface that approximates F(X,Y) given samples f(i,j) over a grid with regular spacing in both the x and y directions. More...

Real	calcValue (const Vec2 &XY, PatchHint &hint) const
	Calculate the value of the surface at a particular XY coordinate. More...

Real	calcValue (const Vec2 &XY) const
	This is a slow-but-convenient version of calcValue() since it does not provide for a PatchHint. More...

UnitVec3	calcUnitNormal (const Vec2 &XY, PatchHint &hint) const
	Calculate the outward unit normal to the surface at a particular XY coordinate. More...

UnitVec3	calcUnitNormal (const Vec2 &XY) const
	This is a slow-but-convenient version of calcUnitNormal() since it does not provide for a PatchHint. More...

Real	calcDerivative (const Array_< int > &derivComponents, const Vec2 &XY, PatchHint &hint) const
	Calculate a partial derivative of this function at a particular point. More...

Real	calcDerivative (const Array_< int > &derivComponents, const Vec2 &XY) const
	This is a slow-but-convenient version of calcDerivative() since it does not provide for a PatchHint. More...

bool	isSurfaceDefined (const Vec2 &XY) const
	The surface interpolation only works within the grid defined by the vectors x and y used in the constructor. More...

Vec2	getMinXY () const
	Return the lowest XY pair for which this surface is defined; that is the point (xmin,ymin). More...

Vec2	getMaxXY () const
	Return the highest XY pair for which this surface is defined; that is the point (xmax,ymax). More...

PolygonalMesh	createPolygonalMesh (Real resolution=1) const
	Create a mesh that can be used to visualize this surface. More...

Statistics
This class keeps track of the number of surface accesses made (using either calcValue() or calcDerivative(), and how many of those were resolved successfully using some or all of the hint information. Methods in this section allow access to those statistics. Note that these statistics include accesses from all users of this surface.
int	getNumAccesses () const
	This is the total number of calls made to either calcValue() or calcDerivative(). More...

int	getNumAccessesSamePoint () const
	This is the number of accesses which specified a point whose information was already available in the hint. More...

int	getNumAccessesSamePatch () const
	This is the number of accesses which specified a new point on the same patch as was already present in the hint, or asked for new information about the same point. More...

int	getNumAccessesNearbyPatch () const
	This is the number of accesses which specified on a point that was not on the patch currently in the hint, but was close enough that we did not have to do a general search. More...

void	resetStatistics () const
	Reset all statistics to zero. More...

Advanced methods
The constructors here assume you have already computed the function values and derivatives. Most users should use the constructors that construct this information automatically from given data points.
	BicubicSurface (const Vector &x, const Vector &y, const Matrix &f, const Matrix &fx, const Matrix &fy, const Matrix &fxy)
	(Advanced) A constructor for a bicubic surface that sets the partial derivatives of the surface to the values specified by fx, fy, and fxy. More...

	BicubicSurface (const Vec2 &XY, const Vec2 &spacing, const Matrix &f, const Matrix &fx, const Matrix &fy, const Matrix &fxy)
	(Advanced) Same, but with regular grid spacing. More...

void	calcParaboloid (const Vec2 &XY, PatchHint &hint, Transform &X_SP, Vec2 &k) const
	(Advanced) For use with Hertz contact at a point Q we need to know the surface normal and principal curvature magnitudes and directions. More...

void	calcParaboloid (const Vec2 &XY, Transform &X_SP, Vec2 &k) const
	(Advanced) This is a slow-but-convenient version of calcParaboloid() since it does not provide for a PatchHint. More...

void	getNumPatches (int &nx, int &ny) const
	(Advanced) Get the number of individual bicubic patches used to form this surface, as the dimensions along each side of a rectangular grid. More...

Geo::BicubicHermitePatch	calcHermitePatch (int x, int y) const
	(Advanced) Select a patch by its (x,y) position in the rectangular grid of individual bicubic patches from which this surface is constructed, returning it as a Hermite patch. More...

Geo::BicubicBezierPatch	calcBezierPatch (int x, int y) const
	(Advanced) Select a patch by its (x,y) position in the rectangular grid of individual bicubic patches from which this surface is constructed, returning it as a Bezier patch. More...

Bookkeeping
Methods in this section are administrative and most users will not need to use them.
bool	isEmpty () const
	Return `true` if this is an empty handle meaning that it does not currently refer to any surface. More...

void	clear ()
	Return this handle to its default-constructed state, meaning that it will not refer to any surface. More...

Detailed Description

This class will create a smooth surface that approximates a two-argument function F(X,Y) from a given set of samples of that function on a rectangular grid with regular or irregular spacing.

This is useful both for function interpolation and to provide height-mapped terrain surfaces. See the related class BicubicFunction if you need to satisfy the SimTK::Function interface. A single BicubicSurface can be shared among multiple accessors and threads once constructed.

A single-patch bicubic surface

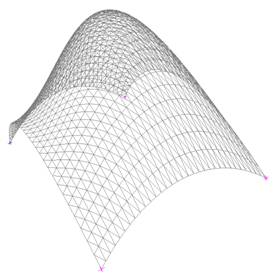
A bicubic surface interpolation is used to approximate the function between the sample points. That is desirable for simulation use because it is continuous up to the second derivative, providing smoothly varying first derivatives, and a very smooth surface. The third derivatives will be discontinuous between grid boundaries; all higher derivatives are zero.

The user need only provide two vectors x and y defining the sample points, and a matrix f that defines the value of the function at each sample (you can think of that as the height Z of the surface over the X-Y plane). If the samples along both axes are regularly spaced, x and y can be defined just by giving the spacing; otherwise, the sample locations are given explicitly.

Usage

The following code generates an unsmoothed and smoothed surface using a 3x4 grid of bicubic patches from a matrix of 4x5 irregularly-spaced sample points:

const int Nx = 4, Ny = 5;
const Real xData[Nx]    = { .1, 1, 2, 4 };
const Real yData[Ny]    = { -3, -2, 0, 1, 3 };
const Real fData[Nx*Ny] = { 1,   2,   3,   3,   2,
                           1.1, 2.1, 3.1, 3.1, 2.1,
                            1,   2,   7,   3,   2,
                           1.2, 2.2, 3.2, 3.2, 2.2 };
const Vector x(Nx,    xData);
const Vector y(Ny,    yData);
const Matrix f(Nx,Ny, fData);
BicubicSurface surfaceThroughSamples(x, y, f);
BicubicSurface smoothedSurface(x, y, f, 1); 
// Evaluate the surface at (.5,.5):
Real val = smoothedSurface.calcValue(Vec2(.5,.5));

When accessing the surface repeatedly, you can significantly improve performance by maintaining a "hint" object that allows for very fast repeated access to the same patch, a very common access pattern. Alternatively, use a BicubicFunction as the interface to your BicubicSurface; in that case the hint is managed for you automatically. Here is an example of explicit hint usage:

PatchHint hint;
val = smoothedSurface.calcValue(Vec2(.5,.6), hint);
val = smoothedSurface.calcValue(Vec2(.51,.61), hint);

Additional methods are provided for obtaining the surface normals, and all the surface partial derivatives. Advanced users can obtain principal curvature directions, and performance statistics, among other specialized functions.

If you want to visualize the surface, you can ask it to generate a polygonal mesh (with optional control over the resolution). That mesh can be used to generate a DecorativeMesh compatible with the Simbody Visualizer. This example creates a mesh of the smoothed surface, then places it on the Ground body so that the Visualizer will pick it up.

PolygonalMesh smoothedMesh = smoothedSurface.createPolygonalMesh();
matter.Ground().addBodyDecoration(Vec3(0), // place at origin
    DecorativeMesh(smoothedMesh)
        .setRepresentation(DecorativeGeometry::Wireframe)
        .setColor(Blue));

Discussion

Graphically if the defining sample vectors and matrices were laid next to each other consistently with how the surface is computed the diagram would look like this:

             y(0)       y(1)    ...   y(ny-1)
            ------     ------         --------
    x(0)  |  f(0,0)     f(0,1)  ...   f(0,ny-1)
    x(1)  |  f(1,0)     f(1,1)  ...   f(1,ny-1)
     .    |    .          .              .
     .    |    .          .              .
     .    |    .          .              .
  x(nx-1) | f(nx-1,0)  f(nx-1,1)    f(nx-1,ny-1)

such that f(i,j)=F(x(i),y(j)).

Note that the each XY location can only have a unique value associated with it – cave-like structures cannot be represented using this interpolation method.

A bicubic surface interpolation requires the partial derivatives fx=Df/Dx, fy=Df/Dy and fxy=Dfx/Dy=D^2f/DxDy at each of the grid points. If you already know those, you can provide them directly. However, in most cases you will only know the sample points and not the derivatives. You can provide just the sample points and BicubicSurface will estimate the derivatives automatically. For the interested reader, these partial derivatives are computed by fitting splines through the points provided, and then taking derivatives of splines.

These splines will pass through the points exactly when the smoothness parameter of the surface is set to 0, and will be interpolated using natural cubic splines, meaning that the curvature will be zero at the boundaries. When the smoothness parameter is greater than zero, the surface will be "relaxed" using the algorithm provided by SplineFitter, and will not exactly pass through the points given, but will smoothly come close to the points. The smoothness parameter can thus be used to generate a surface that smoothly interpolates noisy surface data.

Here is a Wikipedia entry that describes the basic approach: http://en.wikipedia.org/wiki/Bicubic_interpolation

Author: Matthew Millard, Michael Sherman

See also: SplineFitter for implementation notes regarding smoothing.; BicubicFunction

Constructor & Destructor Documentation

◆ BicubicSurface() [1/6]

SimTK::BicubicSurface::BicubicSurface ( )

inline

Construct an uninitialized BicubicSurface handle.

This can be filled in later by assignment.

◆ ~BicubicSurface()

SimTK::BicubicSurface::~BicubicSurface ( )

Destructor deletes the underlying surface if there are no more handles referencing it, otherwise does nothing.

◆ BicubicSurface() [2/6]

SimTK::BicubicSurface::BicubicSurface ( const BicubicSurface & source )

Copy constructor makes a shallow copy of source; the new handle will reference the same underlying surface as does source.

◆ BicubicSurface() [3/6]

SimTK::BicubicSurface::BicubicSurface	(	const Vector &	x,
		const Vector &	y,
		const Matrix &	f,
		Real	smoothness = `0`
	)

Construct a bicubic surface that approximates F(X,Y) given samples f(i,j) with the sample locations in f defined by the vectors x and y.

The smoothness parameter controls how closely the surface approaches the grid points specified in matrix f, with the default being that the surface will pass exactly through those points.

Parameters

[in]	x	Vector of sample locations along the X axis (minimum 4 values). Must be monotonically increasing (no duplicates).
[in]	y	Vector of sample locations along the Y axis (minimum 4 values). Must be monotonically increasing (no duplicates).
[in]	f	Matrix of function values (or surface heights) evaluated at the grid points formed by x and y (dimension x.size() by y.size()), such that f(i,j) is F(x[i],y[j]) where F is the function being approximated here.
[in]	smoothness	A value of 0 will force surface to pass through all of the points in f(x,y). As smoothness increases, the surface will become smoother and smoother but will increasingly deviate from the points stored in matrix f. (Optional, default is 0.)

If your sample points are regularly spaced, use the other constructor.

◆ BicubicSurface() [4/6]

SimTK::BicubicSurface::BicubicSurface	(	const Vec2 &	XY,
		const Vec2 &	spacing,
		const Matrix &	f,
		Real	smoothness = `0`
	)

Construct a bicubic surface that approximates F(X,Y) given samples f(i,j) over a grid with regular spacing in both the x and y directions.

The smoothness parameter controls how closely the surface approaches the grid points specified in matrix f, with the default being that the surface will pass exactly through those points.

Parameters

[in]	XY	A Vec2 giving the (x0,y0) sample location associated with the (0,0) grid position in matrix f.
[in]	spacing	A Vec2 giving regular spacing along the x and y directions; both entries must be greater than 0. The (i,j)th sample location is then taken to be XY + (ispacing[0], jspacing[1]).
[in]	f	Matrix of function values (or surface heights) evaluated at points of the x-y plane regularly sampled using the supplied spacings. Can be rectangular but must have minimum dimension 4x4. Here f(i,j)=F(XY[0]+ispacing[0],XY[1]+jspacing[1]) where F is the function being approximated.
[in]	smoothness	A value of 0 will force surface to pass through all of the points in f. As smoothness increases, the surface will become smoother and smoother but will increasingly deviate from the points stored in matrix f. (Optional, default is 0.)

If your sample points are not regularly spaced, use the other constructor which allows for specified sample points.

◆ BicubicSurface() [5/6]

SimTK::BicubicSurface::BicubicSurface	(	const Vector &	x,
		const Vector &	y,
		const Matrix &	f,
		const Matrix &	fx,
		const Matrix &	fy,
		const Matrix &	fxy
	)

(Advanced) A constructor for a bicubic surface that sets the partial derivatives of the surface to the values specified by fx, fy, and fxy.

Parameters

[in]	x	vector of X grid points (minimum 2 values)
[in]	y	vector of Y grid points (minimum 2 values)
[in]	f	matrix of the surface heights evaluated at the grid formed by x and y (minumum 2x2)
[in]	fx	matrix of partial derivative of f w.r.t to x (minumum 2x2)
[in]	fy	matrix of partial derivative of f w.r.t to y (minumum 2x2)
[in]	fxy	matrix of partial derivative of f w.r.t to x,y (minumum 2x2)

◆ BicubicSurface() [6/6]

SimTK::BicubicSurface::BicubicSurface	(	const Vec2 &	XY,
		const Vec2 &	spacing,
		const Matrix &	f,
		const Matrix &	fx,
		const Matrix &	fy,
		const Matrix &	fxy
	)

(Advanced) Same, but with regular grid spacing.

Member Function Documentation

◆ operator=()

BicubicSurface& SimTK::BicubicSurface::operator= ( const BicubicSurface & source )

Copy assignment is shallow; it makes this handle reference the same underlying surface as does source.

If this handle was currently referencing a different surface, that surface will be destructed if that was the last reference to it.

◆ calcValue() [1/2]

Real SimTK::BicubicSurface::calcValue	(	const Vec2 &	XY,
		PatchHint &	hint
	)		const

Calculate the value of the surface at a particular XY coordinate.

Parameters

[in]	XY	A Vec2 giving the (X,Y) point at which F(X,Y) is to be evaluated.
[in,out]	hint	Information saved from an earlier invocation of calcValue(), calcUnitNormal(), or calcDerivative() that is used to reduce execution time.

Returns: The interpolated value of the function at point (X,Y).

Cost is minimal for repeated access to the same point, and considerably reduced if access is to the same patch. We also take advantage of a regularly-spaced grid if there is one to avoid searching for the right patch.

◆ calcValue() [2/2]

Real SimTK::BicubicSurface::calcValue ( const Vec2 & XY ) const

This is a slow-but-convenient version of calcValue() since it does not provide for a PatchHint.

See the other signature for a much faster version.

◆ calcUnitNormal() [1/2]

UnitVec3 SimTK::BicubicSurface::calcUnitNormal	(	const Vec2 &	XY,
		PatchHint &	hint
	)		const

Calculate the outward unit normal to the surface at a particular XY coordinate.

Parameters

[in]	XY	A Vec2 giving the (X,Y) point at which the normal is to be evaluated.
[in,out]	hint	Information saved from an earlier invocation of calcValue(), calcUnitNormal(), or calcDerivative() that is used to reduce execution time.

Returns: The outward unit normal at point (X,Y).

This requires evaluating the first derivatives of the patch, constructing tangents, finding their cross product and normalizing.

◆ calcUnitNormal() [2/2]

UnitVec3 SimTK::BicubicSurface::calcUnitNormal ( const Vec2 & XY ) const

This is a slow-but-convenient version of calcUnitNormal() since it does not provide for a PatchHint.

See the other signature for a much faster version.

◆ calcDerivative() [1/2]

Real SimTK::BicubicSurface::calcDerivative	(	const Array_< int > &	derivComponents,
		const Vec2 &	XY,
		PatchHint &	hint
	)		const

Calculate a partial derivative of this function at a particular point.

Which derivative to take is specified by listing the input components (0==x, 1==y) with which to take it. For example, if derivComponents=={0}, that indicates a first derivative with respective to argument x. If derivComponents=={0, 0, 0}, that indicates a third derivative with respective to argument x. If derivComponents=={0, 1}, that indicates a partial second derivative with respect to x and y, that is Df(x,y)/DxDy. (We use capital D to indicate partial derivative.)

Parameters

[in]	derivComponents	The input components with respect to which the derivative should be taken. Its size must be less than or equal to the value returned by getMaxDerivativeOrder().
[in]	XY	The vector of two input arguments that define the XY location on the surface.
[in,out]	hint	Information saved from an earlier invocation of calcValue(), calcUnitNormal(), or calcDerivative() that is used to reduce execution time.

Returns: The interpolated value of the selected function partial derivative for arguments (X,Y).

See comments in calcValue() for a discussion of cost and how the hint is used to reduce the cost.

◆ calcDerivative() [2/2]

Real SimTK::BicubicSurface::calcDerivative	(	const Array_< int > &	derivComponents,
		const Vec2 &	XY
	)		const

This is a slow-but-convenient version of calcDerivative() since it does not provide for a PatchHint.

See the other signature for a much faster version.

◆ isSurfaceDefined()

bool SimTK::BicubicSurface::isSurfaceDefined ( const Vec2 & XY ) const

The surface interpolation only works within the grid defined by the vectors x and y used in the constructor.

This function checks to see if an XYval is within the defined bounds of this particular BicubicSurface.

Parameters

[in] XY The vector of exactly 2 input arguments that define the XY location on the surface.

Returns: true if the point is in range, false otherwise.

An attempt to invoke calcValue() or calcDerivative() on an out-of-range point will raise an exception; use this method to check first if you are not sure.

◆ getMinXY()

Vec2 SimTK::BicubicSurface::getMinXY ( ) const

Return the lowest XY pair for which this surface is defined; that is the point (xmin,ymin).

◆ getMaxXY()

Vec2 SimTK::BicubicSurface::getMaxXY ( ) const

Return the highest XY pair for which this surface is defined; that is the point (xmax,ymax).

◆ createPolygonalMesh()

PolygonalMesh SimTK::BicubicSurface::createPolygonalMesh ( Real resolution = 1 ) const

Create a mesh that can be used to visualize this surface.

The default resolution will generate four quads (2x2) per patch. Set resolution to the number of times you want each patch subdivided. The default is 1; set resolution=0 to get just one quad per patch, resolution=3 would give 16 quads (4x4) per patch.

The resulting mesh has its origin at (0,0,0), not at (x[0],y[0],0) as you might expect. X,Y,Z directions match the surface description.

◆ getNumAccesses()

int SimTK::BicubicSurface::getNumAccesses ( ) const

This is the total number of calls made to either calcValue() or calcDerivative().

◆ getNumAccessesSamePoint()

int SimTK::BicubicSurface::getNumAccessesSamePoint ( ) const

This is the number of accesses which specified a point whose information was already available in the hint.

Note that if different information is requested about the point, and that information is not already available, we count that as "same patch" but not "same point". These accesses are resolved with essentially no computation.

◆ getNumAccessesSamePatch()

int SimTK::BicubicSurface::getNumAccessesSamePatch ( ) const

This is the number of accesses which specified a new point on the same patch as was already present in the hint, or asked for new information about the same point.

These accesses are resolved without having to search for the patch, and without having to compute patch information. However, specific point information still must be calculated.

◆ getNumAccessesNearbyPatch()

int SimTK::BicubicSurface::getNumAccessesNearbyPatch ( ) const

This is the number of accesses which specified on a point that was not on the patch currently in the hint, but was close enough that we did not have to do a general search.

This also applies if the point is on an edge since those don't require searching either. So these accesses avoided searching, but still required patch and point information to be computed, which can be expensive.

◆ resetStatistics()

void SimTK::BicubicSurface::resetStatistics ( ) const

Reset all statistics to zero.

Note that statistics are mutable so you do not have to have write access to the surface. Any user of this surface can reset statistics and we make no attempt to handle simultaneous access by multiple threads in any careful manner.

◆ calcParaboloid() [1/2]

void SimTK::BicubicSurface::calcParaboloid	(	const Vec2 &	XY,
		PatchHint &	hint,
		Transform &	X_SP,
		Vec2 &	k
	)		const

(Advanced) For use with Hertz contact at a point Q we need to know the surface normal and principal curvature magnitudes and directions.

This can be viewed as an approximating paraboloid at Q in a frame P where OP=Q, Pz is the outward-facing unit normal to the surface at Q, Px is the direction of maximum curvature and Py is the direction of minimum curvature. k=(kmax,kmin) are the returned curvatures with kmax >= kmin > 0. The equation of the resulting paraboloid in the P frame is -2z = kmax*x^2 + kmin*y^2.

Parameters

[in]	XY	The Vec2 that defines the desired location on the surface such that the contact point Q=F(X,Y).
[in,out]	hint	Information saved from an earlier invocation of this or another hint-using method in this class.
[out]	X_SP	The frame of the paraboloid P, measured and expressed in the surface local frame S. X_SP.p() is Q, X_SP.x() is the calculated direction of maximum curvature kmax; y() is the direction of minimum curvature kmin; z is the outward facing normal at Q.
[out]	k	The maximum (k[0]) and minimum (k[1]) curvatures of the surface (and paraboloid P) at point Q.

◆ calcParaboloid() [2/2]

void SimTK::BicubicSurface::calcParaboloid	(	const Vec2 &	XY,
		Transform &	X_SP,
		Vec2 &	k
	)		const

(Advanced) This is a slow-but-convenient version of calcParaboloid() since it does not provide for a PatchHint.

See the other signature for a much faster version.

◆ getNumPatches()

void SimTK::BicubicSurface::getNumPatches	(	int &	nx,
		int &	ny
	)		const

(Advanced) Get the number of individual bicubic patches used to form this surface, as the dimensions along each side of a rectangular grid.

There are nx X ny patches with indices in [0..nx-1, 0..ny-1].

◆ calcHermitePatch()

Geo::BicubicHermitePatch SimTK::BicubicSurface::calcHermitePatch	(	int	x,
		int	y
	)		const

(Advanced) Select a patch by its (x,y) position in the rectangular grid of individual bicubic patches from which this surface is constructed, returning it as a Hermite patch.

Cost is roughly 110 flops.

◆ calcBezierPatch()

Geo::BicubicBezierPatch SimTK::BicubicSurface::calcBezierPatch	(	int	x,
		int	y
	)		const

(Advanced) Select a patch by its (x,y) position in the rectangular grid of individual bicubic patches from which this surface is constructed, returning it as a Bezier patch.

Cost is roughly 330 flops.

◆ isEmpty()

bool SimTK::BicubicSurface::isEmpty ( ) const

inline

Return true if this is an empty handle meaning that it does not currently refer to any surface.

This is the state the handle will have after default construction or a call to clear().

◆ clear()

void SimTK::BicubicSurface::clear ( )

Return this handle to its default-constructed state, meaning that it will not refer to any surface.

If the handle was referencing some surface, and that was the last reference to that surface, then the surface will be destructed. After a call to clear(), isEmpty() will return true.

The documentation for this class was generated from the following file:

BicubicSurface.h

Classes

Public Member Functions

Detailed Description

Usage

Discussion

Constructor & Destructor Documentation

◆ BicubicSurface() [1/6]

◆ ~BicubicSurface()

◆ BicubicSurface() [2/6]

◆ BicubicSurface() [3/6]

◆ BicubicSurface() [4/6]

◆ BicubicSurface() [5/6]

◆ BicubicSurface() [6/6]

Member Function Documentation

◆ operator=()

◆ calcValue() [1/2]

◆ calcValue() [2/2]

◆ calcUnitNormal() [1/2]

◆ calcUnitNormal() [2/2]

◆ calcDerivative() [1/2]

◆ calcDerivative() [2/2]

◆ isSurfaceDefined()

◆ getMinXY()

◆ getMaxXY()

◆ createPolygonalMesh()

◆ getNumAccesses()

◆ getNumAccessesSamePoint()

◆ getNumAccessesSamePatch()

◆ getNumAccessesNearbyPatch()

◆ resetStatistics()

◆ calcParaboloid() [1/2]

◆ calcParaboloid() [2/2]

◆ getNumPatches()

◆ calcHermitePatch()

◆ calcBezierPatch()

◆ isEmpty()

◆ clear()